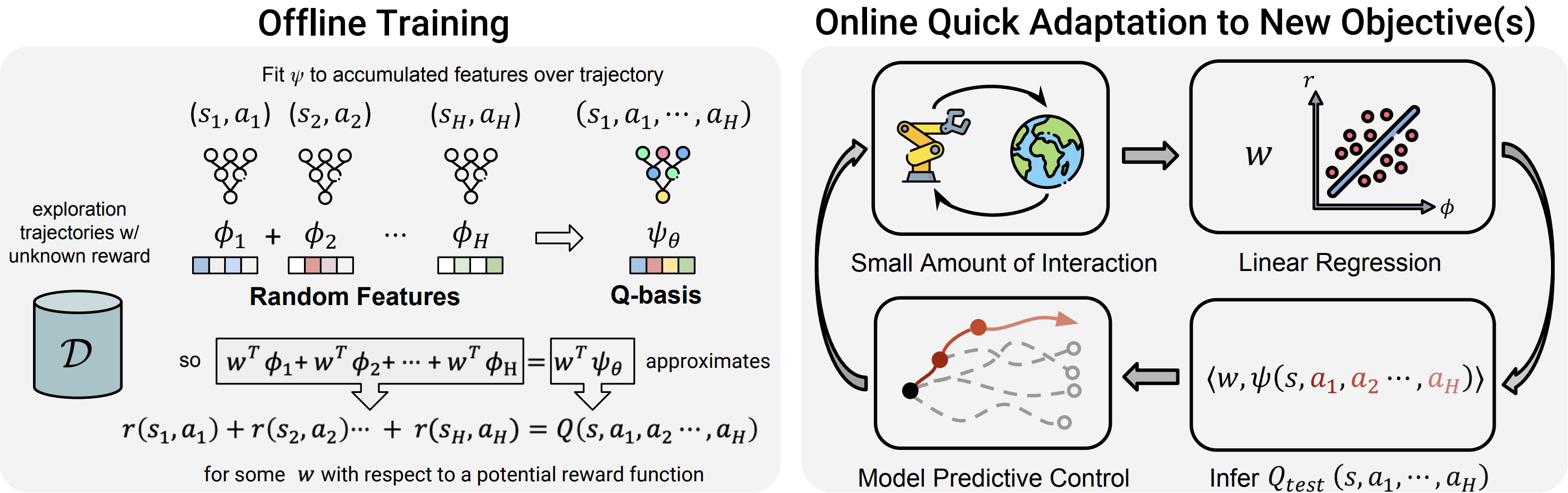
Experiments
Transfer learning to new tasks
We evaluate the ability of RaMP to leverage the knowledge of
shared dynamics from an offline dataset to quickly solve new
tasks with arbitrary rewards. In particular, as shown in the
figure below, we make no assumptions about train/test time task
distribution. A test time task may have reward/goal that's
completely out of distribution, and RaMP can still adapt quickly
unlike goal conditioned RL.

Given this problem setup, we compare RaMP with a variety of
baselines. (1) MBPO is a modelbased RL method that learns a
standard one-step dynamics model and uses actor-critic methods
to plan in the model. We pre-train the dynamics model for MBPO
on the offline dataset. (2) PETS is a model-based RL method that
learns an ensemble of one-step dynamics models and performs MPC.
We pre-train the dynamics model on the offline dataset and use
the cross-entropy method (CEM) to plan. (3) Successor feature
(SF) is a framework for transfer learning in RL as described in
Sec. 1.1. SF typically assumes access to a set of policies
towards different goals along with a learned featurization, so
we provide it with the privileged dataset to learn a set of
training policies. We also learn successor features with the
privileged dataset. (4) CQL : As an oracle comparison, we
compare with a goal-conditioned variant of an offline RL
algorithm (CQL). CQL is a model-free offline RL algorithm that
learns policies from offline data. While model-free offline RL
naturally struggles to adapt to arbitrarily changing rewards, we
provide CQL with information about the goal at both training and
testing time. We evaluate RaMP on a variety of manipulation and
locomotion tasks in simulation. We show that RaMP can learn to
solve tasks with high-dimensional observations and actions, as
well as long horizons.
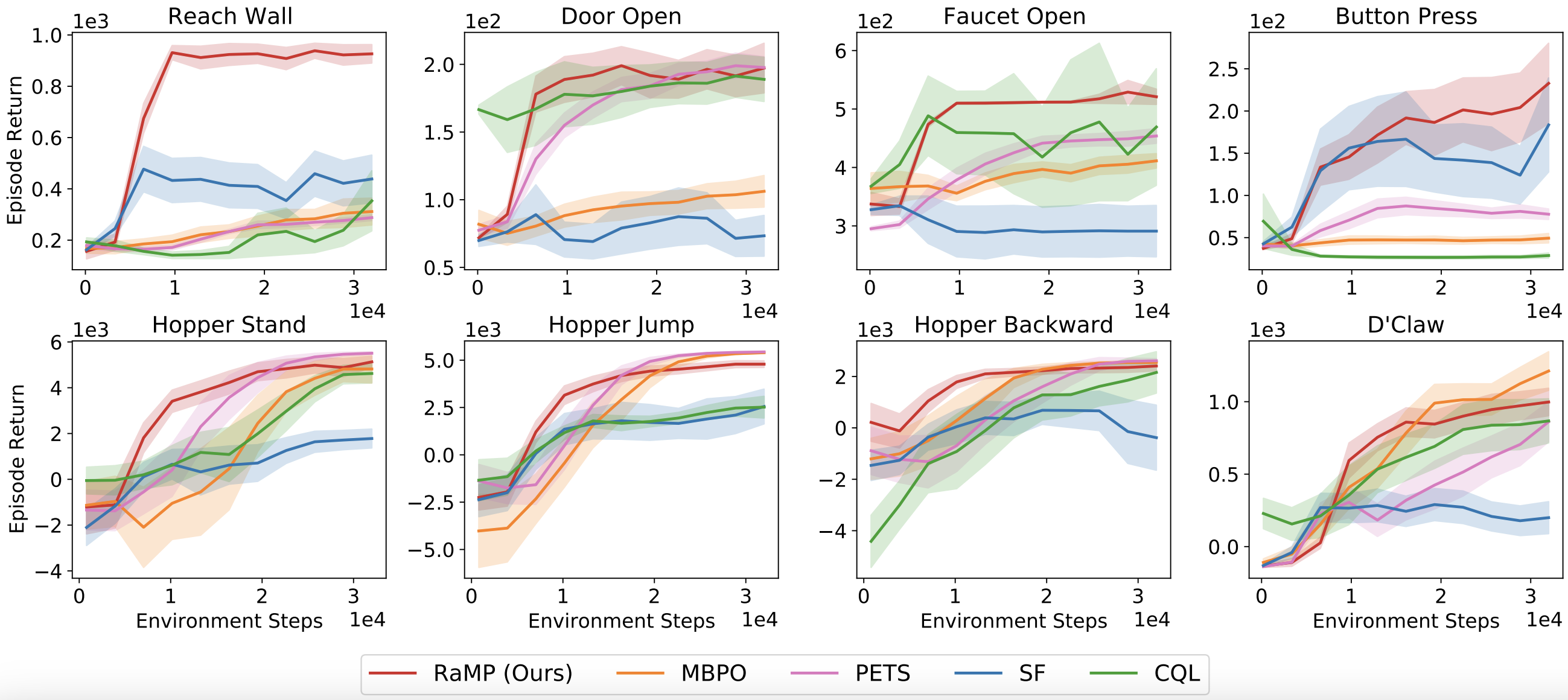
High-dimensional observation and action spaces and long horizons
In particular, we evaluate the ability of our method to scale to
tasks with longer horizons. We consider locomotion domains such
as the Hopper environment from OpenAI Gym. We chose the offline
objectives to be a mixture of skills such as standing,
sprinting, jumping, or running backward with goals defined as
target velocities or heights. The online objectives consist of
unseen goal velocities or heights for standing, sprinting,
jumping or running. RaMP maintains the highest performance when
adapting to novel online objectives, as it avoids compounding
errors by directly modeling accumulated random features. MBPO
adapts at a slower rate since higher dimensional observation and
longer horizons increase the compounding error of model-based
methods. We note that SF is performing reasonably well, likely
because the method also reduces the compounding error compared
to MBPO, and it has privileged information. To understand
whether RaMP can scale to higher dimensional state-action
spaces, we consider a dexterous manipulation domain referred to
as the D’Claw domain in the figure. This domain has a 9 DoF
action space controlling each of the joints of the hand as well
as a 16-dimensional state space including object position. RaMP
consistently outperforms the baselines, and is able to adapt to
out-of-distribution goals at test time.